реш_математика

Решения задач разминочной е-олимпиады по математике.
7 класс
1. Три землекопа за 3 часа выкопали 3 ямы, значит, шесть землекопов за три часа выкопают шесть ям. А шесть землекопов за пять часов еще в 5/3 раза больше, то есть 6 * 5/3=10 ям.
2. Наименьшее число с суммой цифр 2 (сумма цифр не должна равняться самому числу) - 11. Наименьшее число с суммой цифр 11 - 29. Наименьшее число с суммой цифр 29 - 2999. Ответ: 2999.
3. Ответ: 1 банан. Поскольку Сова, Кролик вместе съели 45 бананов, то кто-то из них съел не менее 23 бананов, тогда Винни-Пух съел не менее 24 бананов. Значит Сова, Кролик и Пух съели вместе не менее 69 бананов. Но т.к. Пятачку тоже что-то досталось ,то Сова, Кролик и Пух съели вместе ровно 69 бананов, а Пятачок - 1 банан.
4. 2 см 2 см
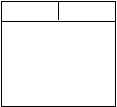wpe3.jpg (1961 bytes) 3, 5 см

4 см

5. Пусть на складе х банок по 0,7 л, а банок по 0,5 л - нет. Тогда банок по 1 л: 2500-х. Общая емкость банок - 1998л., значит 0,7х+1*(2500-х)=1998. Преобразуя получим: 0,3х=502. Т.к. х должно быть целым числом, предположение о том, что на складе нет банок по 0,5л - неверно.
8 класс
1. Среди чисел от 1 до 1984 существует 992 четных числа. Каждое из них дает по крайней мере одну двойку в разложении на простые множители числа 1984!. Две двойки в этом разложении дадут числа, делящиеся на 4 (их всего 496). Далее по 3, 4, 5, 6, 7, 7, 8, 9, 10 двоек соответственно дадут 248, 124, 62, 31, 15, 7, 3 и 1 чисел, делящихся на 8, 16, 32, 64, 128, 256, 512, 1024 соответственно. Сложив полученные числа, мы получим искомый ответ 992 + 496 + 248 + 124 + 62 + 31 + 15 + 7 + 3 + 1=1979.
2. Из второго условия задачи следует, что в каждом из двух баков - первом и втором должно быть не меньше 26 л. бензина. Поэтому общий объем бензина в первых двух баках должен быть не меньше 52 л, а 52>50. Значит, осуществить такой разлив - невозможно.
3. Чему может равняться возраст туристов? Очевидно, одному из чисел: 20, 21, :, 35 (всего 16 вариантов). Поэтому, если предположить, что возраст любых двух туристов различен, то в группе не больше 16 человек. Но по условию задачи их 20. Значит, в группе обязательно есть одногодки.
4.

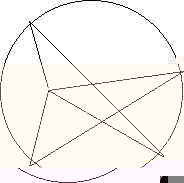wpe4.jpg (5112 bytes) Пусть колодец в т.О. При таком расположении сумма расстояний от домов до колодца - АС+BD. Пусть О' не совпадает с О. О'А + О'С >АС; О'В + О'D > ВD (неравенства треугольника). Значит О'А + О'В + О'С + О'D > АС +ВD

5. (а+1/а) - целое
(а+1/а)^2 - целое
(а + 1 / а) ^ 2 = а ^ 2 + 1 / a ^ 2 + 2 a * 1 / a = а ^ 2 + 1 / a ^ 2 + 2
а ^ 2 + 1 / a ^ 2 = ( а + 1 / а ) ^ 2 - 2
Следовательно, а ^ 2 + 1 / a ^ 2 - целое.
9 класс
1. Число делится на 9, если сумма его цифр делится на 9. Поэтому одна из возможных стратегий для Пети - дополнять на каждом ходу Васину цифру до 9. Т.е., если Вася пишет "0", Петя пишет "9", если Вася пишет "1", то Петя пишет "8" и т.д.
2. После каждого боя из соревнований выбывает один боксер, проигравший в этом бою. Поскольку к концу соревнований выбыть должны все, кроме победителя, то должно быть 49 боев, независимо от того, как составляется расписание.
3.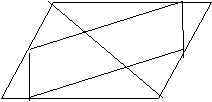 wpe5.jpg (3945 bytes) Пусть О - центр АВСD. При симметрии относительно О точки А и С, а также В и D попарно переходят друг в друга Прямая а переходит в параллельную ей прямую, проходящую через точку С - т.е. в прямую с. Аналогично, прямая b переходит в прямую d. Значит "внешний" параллелограмм переходит в себя, т.е. т. О является его центром.
4. Любой общий делитель чисел х=9m+7n и y=3m+2n должен быть также делителем чисел x-2y=n и 7y-2x=3m. Поскольку числа m и n не имеют общих делителей кроме 1, то любой общий делитель чисел n и 3m должен быть делителем числа 3. Поэтому он не может быть больше 3. Покажем, что равняться 3 он может. Пусть m=1 n=3, тогда х=30, у=9 - НОД=3
5. 10/7=1+3/7. Значит х=1, а у+1/2=7/3; 7/3=2+1/3; х=1, у=2, z=3.
10 класс
1. Число делится на 9, если сумма его цифр делится на 9. Поэтому одна из возможных стратегий для Пети - дополнять на каждом ходу Васину цифру до 9. Т.е., если Вася пишет "0", Петя пишет "9", если Вася пишет "1", то Петя пишет "8" и т.д.
2. После каждого боя из соревнований выбывает один боксер, проигравший в этом бою. Поскольку к концу соревнований выбыть должны все, кроме победителя, то должно быть 49 боев, независимо от того, как составляется расписание.
3. wpe5.jpg (3945 bytes)

Пусть О - центр АВСD. При симметрии относительно О точки А и С, а также В и D попарно переходят друг в друга Прямая а переходит в параллельную ей прямую, проходящую через точку С - т.е. в прямую с. Аналогично, прямая b переходит в прямую d. Значит "внешний" параллелограмм переходит в себя, т.е. т. О является его центром.

4. Любой общий делитель чисел х=9m+7n и y=3m+2n должен быть также делителем чисел x-2y=n и 7y-2x=3m. Поскольку числа m и n не имеют общих делителей кроме 1, то любой общий делитель чисел n и 3m должен быть делителем числа 3. Поэтому он не может быть больше 3. Покажем, что равняться 3 он может. Пусть m=1 n=3, тогда х=30, у=9 - НОД=3
5. Пусть х и у - данные числа. Условие х+у<ху можно переписать в виде (у-1)(х-1)>1. Откуда очевидно, что х>1, у>1, неравенство о среднем арифметическом и среднем геометрическом для чисел х-1 и у-1 дает (х-1)+(у-1)>=2*корень((х-1)(у-1))>2. Откуда х+у>4.
11 класс
1. Пусть f(x)=ax²+b₁x+c₁, g(x)=ax²+b₂x+c₂, тогда f(x)+ g(x )=2ax²+(b₁+b₂)x+(c₁+c₂) и по теореме Виета (или из формулы корней квадратного уравнения) сумма корней f(x) равна (-b₁/a), сумма корней g(x) равна (-b₂/a), следовательно, -b₁/a-b₂/a=0, откуда -(b₁+b₂)/2=0, а это - сумма корней f(x)+ g(x ).
2. Пусть х - количество толстых, тогда количество тонких равно 58-х, и они вместе принесли 14(58-х) пончиков. Пусть каждый толстый получил по n пончиков, тогда 14(58-х)= nx. Преобразуя, получаем, что (n+41)х=14*58. Значит, х - делитель числа 14*58=2*2*7*29. Подставляявместо х все делители этого числа, меньшие 58 (а именно, 1, 2, 4, 7, 14, 28 и 29), можно убедиться, что условию удовлетворяют толье=ко х=28 и х=29, а для остальных получается, что 15х (число пончиков, принесенных толстыми) не делится на 58-х (количество тонких).
3. 41*271=11111. В любом 35-значном числе без нулей и пятерок есть цифра, которая встречается не менее 5 раз, т.к. 35/8=4(3 в остатке). Вычеркнув все цифры, кроме пяти одинаковых, получим число, кратное 11111, которое кратно 41.
4. Теорема синусов, примененная к треугольникам АВС и АDС, дает AD/sinACD=DC/sinDAC, AB/sinACB=BC/sin BAC, или AD/DC=sinACD/sinDAC, AB/BC=sinACB/sinBAC. Учитывая условие задачи и то ,что углы DAC и BAC равны, получаем sinACD=sinACB. Так как ACD и ACB не равны, то последнее равенство означает, что их сумма равна 180⁰. Значит, больший из них - угол ACB - тупой.
5. Рассмотрим самого высокого солдата в некоторой неправильной шеренге. Докажем, что после него могут стоять не более двух солдат. Для этого предположим противное, что после него стоят по крайней мере трое. Если они стоят по росту в порядке возрастания, то это противоречит условию неправильности шеренги. Если же какие-то двое из них стоят в порядке убывания, то они вместе с самым высоким солдатом образуют тройку стоящих по росту солдат, что опять противоречит условиюнеправильности шеренги. Полученное в обоих случаях противоречиедоказывает сформулированное утверждение. Аналогичные рассужденияпоказывают, что и перед самым высоким солдатом в неправильной шеренге могут стоять не более двух солдат, и что то же самое верно для самого низкого солдата.
а) обозначим солдат буквами А, В, С и D (по росту). Приведенное выше рассуждение показывает, что в неправильной шеренге солдаты А и D должны стоять в середине, а солдаты В и С, тем самым, по краям. Таким образом, мы можем получить 4 неправильных шеренги: BADC, BDAC, CADB, CDAB.
б) Из приведенного выше рассуждения следует, что в неправильной шеренге из пяти солдат самый высокий должен стоять посередине (на третьем месте), то же самое можо утверждать и про самого низкого. Значит, неправильной шеренги из пяти солдат построить нельзя.